
So that lower bound isĢ.1 standard deviations below the mean, or you could say it has a 624 minus 750 is equal to, and then divide by 60, is equal to negative 2.1. And so what is that going to be? I'll get my calculator out for this one, don't wanna make a careless error. The z-score for 624 is going to be equal to 624 minus the mean of 750, all of that over 60. So now let's do the same exercise but do it for the proportion Is right over here, it's a zero, so this is the proportion that is less than $768. But we're at 0.3, so we're going to be in this row, and our hundredths place To our hundredths place, that's what these other columns give us. And so this is 0.3, this first column, and we've done this in other videos, this goes up until the tenths place for our z-score, and then if we wanna go For that, we take out a z-table, get our z-table.

So that is the z-scoreįor this upper bound. So this is going to be equal to 18 over 60, which is the same thing as six over, let's see if we divide the numerator and the denominator by three, 6/20, and this is the same thing as 0.30. I'll write it like that, is going to be 768 minus 750 over the standard deviation, over 60. And so then we can subtract this red area from the proportion that is less than 768 to get this area in between. That will be negative 2 point something, and we will use the z-table again to figure out the proportion Then we'll figure out the z-score for 624. We're even going to figure out the stuff that's below 624. So essentially we're going to figure out this entire area. The way we are going to approach it, we're going to figure out the z-score for 768, it's going to be positive because it's above the mean, and then we're going to useĪ z-table to figure out, what proportion is below 768.
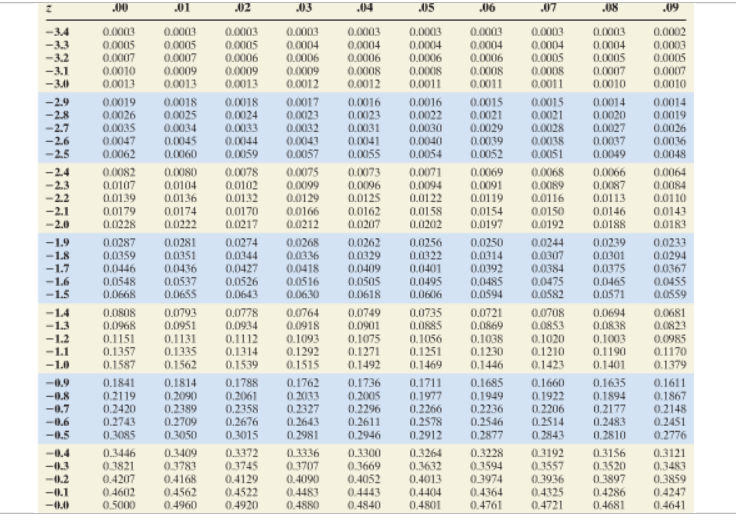
And so what proportion areīetween those two values? So we wanna find essentially the area under this distributionīetween these two values. And 768 would put us right at about right at about there, and once again this is So the lower bound, $624, that's going to actually be more than another standard deviation less, so that's going to be right around here. And then they tell us, what proportion of laptop prices are between $624 and $768. One standard deviation below the mean would put us right about there, and that would be 750 minus $60, which would be $690.
#Standard normal table for critical values plus#
So that means one standardĭeviation above the mean would be roughly right over here, and that would be 750 plus 60. They also tell us that we haveĪ standard deviation of $60. And we have the mean right in the center. It should be symmetric, so I'm making it as symmetricĪs I can hand draw it. This is just my hand-drawn sketch of a normal distribution. So we have a normalĭistribution for the prices. What proportion of laptop prices are between $624 and $768? So let's think about what they are asking.
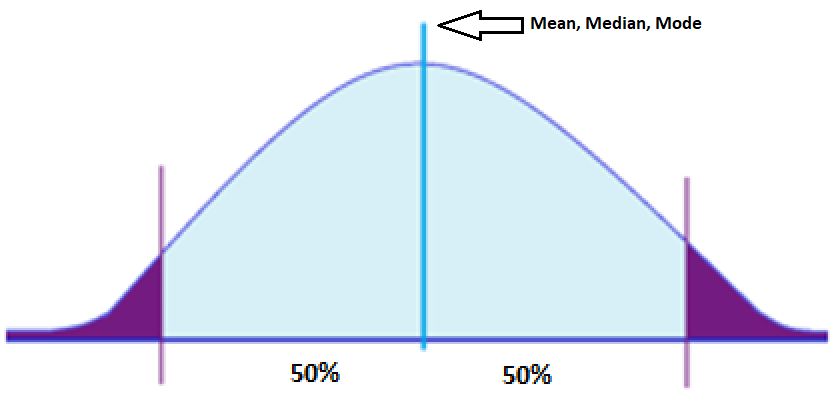
With a mean of $750 and a standard deviation of $60. A set of laptop prices are normally distributed


 0 kommentar(er)
0 kommentar(er)
